들쮜의 개발자일지

https://school.programmers.co.kr/learn/courses/30/lessons/178871

파이썬으로만 알고리즘을 풀다보니 같은 로직을 자바에서는 어떻게 구현해야할지 몰라, 기초 단계부터 다시 공부하고 있습니다.

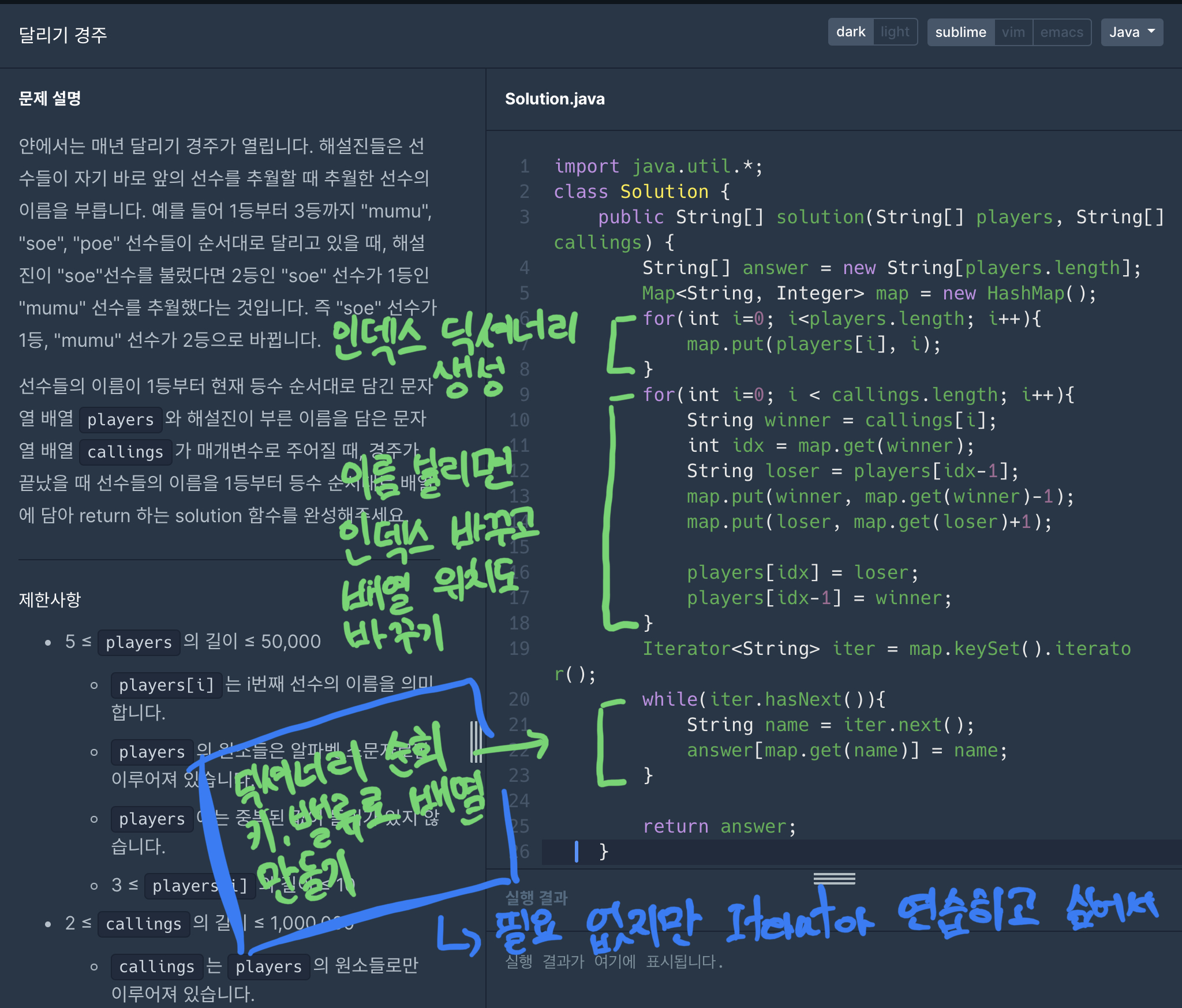
달리기 경주는 학생들의 리스트가 주어지고, 이름이 불려지면 불려진 학생의 인덱스와 그 이전의 인덱스 값을 교환하는 간단한 문제입니다.

프로그래머스에서 바로 구현을 하니, 아이패드에서도 블루투스 키보드 하나로 바로 코딩 문제를 풀 수 있어 매우 행복합니다

아이패드를 살까 말까 고민했었는데, 정말 개발자라면 무조건 사시는 걸 추천합니다 가지고 다니는 것도 훨씬 편하고, 생각 날 때마다 알고리즘 문제를 풀 수 있는 장점이 있습니다.

해당 문제는 호명한 이름의 인덱스 값을 찾는 과정에서 시간이 매우 오래 걸리게 됩니다.

총 100만번 인덱스를 찾아야하는데, 길이가 5만인 배열이니 인덱스를 찾는데에만 100만 * 5만번이나 연산을 수행하니 말이죠.

그래서 딕셔너리가 필요한데, 자바에서는 딕셔너리를 Map 이라는 자료구조를 이용해 구현합니다.

HashMap 으로 딕셔너리를 만든 뒤 각 이름별 인덱스를 담아두고, 호명한 이름의 인덱스는 하나 줄이고 호명한 이름의 바로 이전 인덱스에 있는 친구의 이름은 하나 늘리는 방식으로 인덱스를 계속 바꿔주면, 인덱스를 한번에 접근할 수 있습니다.

Map 자료구조는 put으로 key value값을 넣어주고, get(Key)로 value를 가져올 수 있습니다.

그리고, Map의 키들을 가져오는 keySet() 메서드에서 반환되는 Set은 iterable하지 않으므로 Iterator를 사용하여 순회를 해주어야 합니다.

https://www.acmicpc.net/problem/2613

• 왼쪽부터 차례대로 숫자구슬을 묶으면서 묶여있는 구슬의 합의 최댓값이 최소가 되게 하는 문제.
• 처음엔 간단하게 조합을 이용하여 풀어보려고 했지만, 골드2 문제답게 조합으로 풀면 시간 초과가 나게 된다.
• 이분탐색과 그리디 알고리즘을 이용하여 시간을 낮추어 풀 수 있었다.

1. 숫자구슬 묶음의 개수는 최소 1개 최대 N개가 된다
2. 숫자구슬 묶음을 1개로 두었을 때 최대값은 리스트의 전체 합 즉, sum(n_lst)가 될 것이고, 숫자구슬 묶음을 N개로 두었을 경우 최대값은 리스트 요소 중 최대값 max(n_lst)가 될 것이다
3. 결국 숫자구슬 묶음의 최댓값은 max(n_lst) <= X sum(n_lst)가 될 것이기 때문에 해당 값이 이분탐색으로 구한뒤 최댓값으로 가능한지 그리디 알고리즘을 이용하면 풀면 되는 문제였다.

** 이분탐색을 사용하기 위해 start, end값 설정해주기 **

N, M = map(int, input().split())

n_lst = list(map(int, input().split()))

# 이분탐색을 하기 위해 start와 end값을 찾아야 함
# start값은 1개를 담았을 경우의 최댓값
# end값은 한번에 모든 것을 담았을 경우의 최댓값
# M개의 묶음을 만들어 값을 만들어낼 수 있는 경우를 찾았더라도 최댓값 중 최솟값을 찾아야 하므로 더 낮춰야 함 (end값 낮추기)
start = max(n_lst)
end = sum(n_lst)
min_ans = int(1e9)

** 이분탐색을 돌리면서 최댓값이 가능한지 체크해주고, 그리디 알고리즘을 이용하여 M개의 묶음이 가능한지를 체크 **

• 1, 2, 3, 4, 5 이 구슬들 중 현재 최댓값이 가능한지 체크하는 숫자를10이라고 정해두었다고 생각해보자
• (1, 2, 3, 4) (5) 이렇게 묶음을 나눌 수 있는데, 이 때 만약 내가 구슬을 3개의 묶음으로 만들고자했다면 4개의 구슬을 분할해주면 된다. 그렇기 때문에 내가 묶고 싶은 묶음의 개수 M개보다 작은 경우에도 M개의 묶음이 가능하게 된다.

while start <= end:
    mid = (start + end) // 2
    cnt = 0 #묶음의 개수
    sum = 0 #현재 묶음의 값
    sum_lst = []
    cnt_lst = []
    for i in range(len(n_lst)):
        check = sum + n_lst[i] #현재 묶음에 구슬을 추가로 넣을 수 있는지 체크
        if check > mid: #만약 현재 묶음에 구슬을 추가로 넣을 수 없다면
            cnt_lst.append(cnt) #현재 구슬의 개수와 값을 넣어두고
            sum_lst.append(sum)
            sum = 0 #묶음 구슬의 개수와 값을 초기화시켜준다
            cnt = 0
        # 그런 뒤 다시 값과 개수를 늘려주면 그리디 알고리즘 완료        
        sum += n_lst[i]
        cnt += 1
    #반복문의 마지막은 값과 개수를 늘려주는 것으로 끝나므로 마지막에 추가해준 값과 개수까지 append로 따로 넣어준다.
    sum_lst.append(sum)
    cnt_lst.append(cnt)

** 그리디 알고리즘이 끝났으면 해당 묶음의 개수를 체크하고, 원하는 M개보다 작거나 같으면 개수와 값을 갱신해준다. **

    if len(sum_lst) <= M: # 만들어진 개수가 M보다 작거나 같다면 해당 값으로 묶음을 만들 수 있다

        end = mid - 1 # 좀 더 작은 최댓값으로도 묶음을 만들 수 있는지 체크하기 위해 end = mid - 1

        if max(sum_lst) < min_ans:
            min_ans = max(sum_lst) 
            min_cnt = cnt_lst
    else:
        start = mid + 1
print(min_ans)

** 이제 추가로 작업을 해주어야 할 것은 묶음이 M개보다 작을 경우의 체크이다 **

while len(min_cnt) != M: #묶음의 개수가 같아질 때 까지
   if min_cnt[i] == 1 : # 묶음 안의 구슬 개수가 1개일 경우 
       i += 1 #다음 구슬 체크
   else : #묶음 안의 구슬 개수가 1개를 초과할 경우
       min_cnt[i] -= 1 #해당 묶음의 구슬 개수를 하나 줄이고
       min_cnt.insert(i+1, 1) #그 묶음의 바로 앞에 추가로 구슬 묶음을 만들어준다.
print(*min_cnt)

** 최종코드 **

N, M = map(int, input().split())

n_lst = list(map(int, input().split()))

# 이분탐색을 하기 위해 start와 end값을 찾아야 함
# start값은 1개를 담았을 경우의 최댓값
# end값은 한번에 모든 것을 담았을 경우의 최댓값
# M개의 묶음을 만들어 값을 만들어낼 수 있는 경우를 찾았더라도 최댓값 중 최솟값을 찾아야 하므로 더 낮춰야 함 (end값 낮추기)
start = max(n_lst)
end = sum(n_lst)
min_ans = int(1e9)

while start <= end:
    mid = (start + end) // 2
    cnt = 0 #묶음의 개수
    sum = 0 #현재 묶음의 값
    sum_lst = []
    cnt_lst = []
    for i in range(len(n_lst)):
        check = sum + n_lst[i] #현재 묶음에 구슬을 추가로 넣을 수 있는지 체크
        if check > mid: #만약 현재 묶음에 구슬을 추가로 넣을 수 없다면
            cnt_lst.append(cnt) #현재 구슬의 개수와 값을 넣어두고
            sum_lst.append(sum)
            sum = 0 #묶음 구슬의 개수와 값을 초기화시켜준다
            cnt = 0
        # 그런 뒤 다시 값과 개수를 늘려주면 그리디 알고리즘 완료
        sum += n_lst[i]
        cnt += 1
    #반복문의 마지막은 값과 개수를 늘려주는 것으로 끝나므로 마지막에 추가해준 값과 개수까지 append로 따로 넣어준다.
    sum_lst.append(sum)
    cnt_lst.append(cnt)

    if len(sum_lst) <= M: # 만들어진 개수가 M보다 작거나 같다면 해당 값으로 묶음을 만들 수 있다

        end = mid - 1 # 좀 더 작은 최댓값으로도 묶음을 만들 수 있는지 체크하기 위해 end = mid - 1

        if max(sum_lst) < min_ans:
            min_ans = max(sum_lst)
            min_cnt = cnt_lst
    else:
        start = mid + 1
print(min_ans)
i = 0

while len(min_cnt) != M: #묶음의 개수가 같아질 때 까지
   if min_cnt[i] == 1 : # 묶음 안의 구슬 개수가 1개일 경우
       i += 1 #다음 구슬 체크
   else : #묶음 안의 구슬 개수가 1개를 초과할 경우
       min_cnt[i] -= 1 #해당 묶음의 구슬 개수를 하나 줄이고
       min_cnt.insert(i+1, 1) #그 묶음의 바로 앞에 추가로 구슬 묶음을 만들어준다.
print(*min_cnt)

https://www.acmicpc.net/problem/1107

• 채널이 50만번까지 있지만, 채널 버튼을 누르는건 500000을 누르더라도 5, 0, 0, 0, 0, 0 6번밖에 되지 않기 때문에 브루트포스를 사용해 구할 수 있음을 캐치해야했던 문제
• 처음엔 누를 수 있는 채널들 중 가장 주어진 채널 값과 가장 가까운 값을 한번에 찾는 방법을 생각해 그리디 알고리즘으로 풀어보려고 했지만, 계속 반례가 등장하는 바람에 포기할 수 밖에 없었다.

** 주요 포인트 **

• 그리디 알고리즘으로 풀 경우 자릿수가 변하는 경우도 체크를 해주어야 했고, 낮은 값에서 올라가는게 유리한지, 높은 값에서 내려가는게 유리한지도 체크를 해주어야 했다.
• 자릿수도 자릿수를 늘린 뒤 줄여 가는 방법 ex) 999로 가기 위해 1000에서 내려가기, 자릿수를 줄인 뒤 늘려가는 방법 ex) 9에서 11로 가기, 같은 자릿수더라도 작은 숫자에서 올리기 ex) 8000으로 가기위해 9221 을 눌러야 하는 경우가 있고 7779를 눌러야 하는 경우가 있다.
• 로직이 잘못된 걸 수도 있지만 이 경우들을 고려해주어도 계속 놓치는 반레들이 생겨났고, 결국 브루트포스로 문제를 풀 수 밖에 없었다
• 채널 100번에서 시작하므로 버튼을 가장 많이 누르게 되는 경우(모든 숫자가 고장났을 경우) 채널 최댓값인 50만까지 가는데 49900이 들게 되지만 50만에서 시작할 경우 0까지 탐색을 해주기 위해서 그냥 반복을 50만번 수행하도록 했다.

코드 공유

S = input()
N = int(input())
ans = -1
min_ans = 9999999
if N != 0 :
    n_lst = list(map(int, input().split()))
    move = 0
    for move in range(500000) :
        plus_number = int(S) + move #채널 하나를 올려보고 그곳에서 접근할 수 있는지 체크
        minus_number = int(S) - move #채널 하나를 내려보고 그곳에서 접근할 수 있는지 체크
        for i in str(plus_number): # 해당 채널에 이동이 가능하다면 더 move할 필요없이 break
            if int(i) in n_lst :
                break
        else :
            plus_number = abs(int(S) - plus_number) + len(str(plus_number))
            min_ans = min(min_ans, plus_number)

        if minus_number >= 0 :
            for i in str(minus_number):
                if int(i) in n_lst:
                    break
            else :
                minus_number = abs(int(S) - minus_number) + len(str(minus_number))
                min_ans = min(min_ans, minus_number)

        move +=1

else :
    min_ans = len(S)
print(min(abs(100-int(S)), min_ans)) # 100에서 이동하는 것과 구해놓은 채널에서 이동하는 것중 작은 값 출력

https://www.acmicpc.net/problem/22856

• 중위순회를 하면서 거쳐갔던 노드들을 카운트하는 문제
• 재귀연산을 통해 전위, 중위, 후위 순회를 표현하는 법은 배웠지만, 그 순회를 이용해서 다른 문제를 푸는 문제는 처음이었더라 시간이 좀 걸렸던 문제

• 중위 순회에서 우리가 알 수 있는건, 트리의 가장 왼쪽 노드와 그 노드의 부모노드 그리고 리프노드 값이다!
• 유사 중위 순회에서 대부분의 값들은 다시 자기자신으로 돌아오지만, 리프노드를 호출한 함수는 돌아오지 않는다는 걸 체크

핵심코드

def inorder(t):
    global cnt, ans
    if t :
        left = inorder(c1[t])
        if left :
            cnt += 2
        if t == leaf_node :
            return -1
        right = inorder(c2[t])
        if right == -1 :
             cnt += 1
             return -1
        elif right :
            cnt += 2

        return t
    else :
        return 0

https://www.acmicpc.net/problem/17069

분명 BFS로 파이프 옮기기1은 BFS로 풀 수 있는 문제라고 하셨는데...... 결국 DP로 접근해서 풀고,

DP로 풀었으니, 파이프 옮기기2도 가뿐하게 풀 수 있었기에 뿌듯했습니다.

하지만 DP로 어떻게 접근해야 할 지 생각하느라 잠을 설친걸 생각하면.. 아직 멀었다는 생각이 듭니다

그래도 혼자 생각해낸게 어디냐며 굉장히 뿌듯하게 풀은 문제입니다.

** 소스코드는 더보기를 클릭해서 확인해주세요 **

1. DP 접근의 시작

• ㅡ 모양은 0, \ 모양은 1, ㅣ 모양은 2의 상태로 두었습니다.
• 0에서는 0과 1로 갈 수 있지만 2로 갈 수 없고, 1은 0과 1 2 모두 갈 수 있고, 2는 2와 1로 갈 수 있습니다
• 처음엔 무턱대고 이전 값의 경우의수를 체크하여 더해주려고 했지만 이전 값의 경우의수가 있더라도 내 칸으로 올 수 없다는 경우가 발생한다는 걸 깨달았습니다. (내 왼쪽에 파이프가 올 수 있는 경우의 수가 있지만 그 파이프의 상태가 2라면? 오른쪽으로는 못오잖아..?) 
• 그래서 파이프의 상태까지 담아줄 방법을 고민하게 됩니다.

N = int(input())

board = [list(map(int, input().split())) for _ in range(N)]

#경우의수를 담아줄 memo리스트 추가
#그냥 경우의수를 체크하는게 아니라 어떤 상태로 현재 값으로 올 수 있는지를 체크해야한다
# 왜냐면 현재 값에서 0상태로 몇개 1상태로 몇개 2상태로 몇개 올 수 있는지 체크해야만
# 현재값으로 올 수 없는 경우의수가 있기 때문
# i, j좌표에 각 상태별 경우의수를 담는 배열이 하나더 필요하므로 i,j,k 세개의 배열이 필요할 것 같다

memo = [[[0] * 3 for _ in range(N)] for _ in range(N)]

for c in range(N-1): #첫째줄에는 모두 0상태로 들어갈 수 있음
    if board[0][c+1] != 1 :
        memo[0][c+1][0] += 1
    else :
        break

2. 각 칸에 올 수 있는 조건 확인하기

• 다시 처음으로 돌아가 생각해보았는데, 생각해보니 첫 번째 줄에 파이프가 ㅡ 모양(0상태)으로밖에 들어가지 못한다는걸 발견합니다.
• 그것을 발견하고 나니 2번째 칸에는 \(1)모양으로밖에 갈 수 없다는 것도 보이구요
• 또 보니까, 0열과 1열은 첫째줄을 제외하면 사용하지도 못합니다.
• 아!! 각 상태별로 조건들이 보입니다
• 각 칸은 올 수 있는 상태가 정해져있고, 또 1번 상태의 경우에는 이동할 칸의 위와 왼쪽이 비어있어야합니다.
• 모든 조건들을 다 적어주도록 합니다. (1부터 시작할 것이기 때문에 사실 2, 3번째 조건은 필요 없는 조건이긴 하지만요)

# 다음부터는 내 왼쪽과, 위, 그리고 왼쪽 위의 값에 따라 자동으로 경우의수가 증가
for i in range(1, N):
    for j in range(1, N):
        if board[i][j] == 0:
            #왼쪽 위가 존재하는데 상태가 0,1,2이라면 1상태로 올 수 있음
            #단 1상태로 오려면 무조건 올 수 있는게 아니라 위와 왼쪽 공간이 비어있어야함
            if 0 <= i -1 < N and 0 <= j -1 < N and board[i-1][j] == 0 and board[i][j-1] == 0:
                pass
            #위가 존재하는데 1이나 2상태라면 2로 올 수 있음
            if 0 <= i -1 < N :
                pass
            #왼쪽이 존재하는데 0이나 1상태라면 0으로 올 수 있음
            if 0 <= j -1 < N :
                pass

3. 경우의수 체크

• 이제 각 칸들이 들어올 수 있는 조건들을 체크해주었으니 상태값에 따른 경우의수를 넣어주어야 합니다.
• 만약 왼쪽 칸에 파이프가 올 수 있는 경우의 수가 존재했더라도 그 파이프가 2상태라면 올 수 없으니까요.
• 모든 칸의 경우의수를 상태별로 나누어 놓았으니 내 칸으로 올 때 어떤 상태로 오는지도 같이 넣어줍니다.
• 파이프가 왼쪽에 있다면 0가 1상태인 파이프가 0상태인 파이프로 변해서 제 자리로 올 수 있을것이고
• 파이프가 왼쪽위에 있다면 0, 1, 2상태의 파이프가 1상태인 파이프로 변해서 올 수 있을 것이고
• 파이프가 위에 있다면 1과 2상태의 그래프가 2상태인 파이프로 변해서 올 수 있겠죠

# 다음부터는 내 왼쪽과, 위, 그리고 왼쪽 위의 값에 따라 자동으로 경우의수가 증가
for i in range(1, N):
    for j in range(1, N):
        if board[i][j] == 0:
            #왼쪽 위가 존재하는데 상태가 0,1,2이라면 1상태로 올 수 있음
            #단 1상태로 오려면 무조건 올 수 있는게 아니라 위와 왼쪽 공간이 비어있어야함
            if 0 <= i -1 < N and 0 <= j -1 < N and board[i-1][j] == 0 and board[i][j-1] == 0:
                memo[i][j][1] += memo[i-1][j-1][0] + memo[i-1][j-1][1] + memo[i-1][j-1][2]
            #위가 존재하는데 1이나 2상태라면 2로 올 수 있음
            if 0 <= i -1 < N :
                memo[i][j][2] += memo[i-1][j][1] + memo[i-1][j][2]
            #왼쪽이 존재하는데 0이나 1상태라면 0으로 올 수 있음
            if 0 <= j -1 < N :
                memo[i][j][0] += memo[i][j-1][0] + memo[i][j-1][1]

이제 마지막 칸까지 도착한 상태별 경우의수를 모두 더해주면 답이 됩니다.

전체 코드

N = int(input())

board = [list(map(int, input().split())) for _ in range(N)]

#경우의수를 담아줄 memo리스트 추가
#그냥 경우의수를 체크하는게 아니라 어떤 상태로 현재 값으로 올 수 있는지를 체크해야한다
# 왜냐면 현재 값에서 0상태로 몇개 1상태로 몇개 2상태로 몇개 올 수 있는지 체크해야만
# 현재값으로 올 수 없는 경우의수가 있기 때문
# i, j좌표에 각 상태별 경우의수를 담는 배열이 하나더 필요하므로 i,j,k 세개의 배열이 필요할 것 같다

memo = [[[0] * 3 for _ in range(N)] for _ in range(N)]

for c in range(N-1): #첫째줄에는 모두 0상태로 들어갈 수 있음
    if board[0][c+1] != 1 :
        memo[0][c+1][0] += 1
    else :
        break

# 다음부터는 내 왼쪽과, 위, 그리고 왼쪽 위의 값에 따라 자동으로 경우의수가 증가
for i in range(1, N):
    for j in range(1, N):
        if board[i][j] == 0:
            #왼쪽 위가 존재하는데 상태가 0,1,2이라면 1상태로 올 수 있음
            #단 1상태로 오려면 무조건 올 수 있는게 아니라 위와 왼쪽 공간이 비어있어야함
            if 0 <= i -1 < N and 0 <= j -1 < N and board[i-1][j] == 0 and board[i][j-1] == 0:
                memo[i][j][1] += memo[i-1][j-1][0] + memo[i-1][j-1][1] + memo[i-1][j-1][2]
            #위가 존재하는데 1이나 2상태라면 2로 올 수 있음
            if 0 <= i -1 < N :
                memo[i][j][2] += memo[i-1][j][1] + memo[i-1][j][2]
            #왼쪽이 존재하는데 0이나 1상태라면 0으로 올 수 있음
            if 0 <= j -1 < N :
                memo[i][j][0] += memo[i][j-1][0] + memo[i][j-1][1]

print(sum(memo[N-1][N-1]))

 - 문제 설명 -

압축은 K(Q)은 Q * K를 의미합니다. 즉 3(5) = 555 가 됩니다.

K는 한자리 정수입니다. 그렇기 때문에 53(5) = 5가 53개 있는 것이 아니라 5 + 3(5) , 5555 가 됩니다.

압축되지 않은 문자열의 길이를 출력해야 하는데, 주의해야할 점은 압축되지 않은 문자열의 길이가 무려 21억이라는 것

복습할 문제 선정 이유 :

• 압축되지 않은 문자열의 길이가 터무니 없게 높게 주어진 경우, 문자열을 압축해제 해서 풀어나가며 진행할 경우 시간도 오래 걸리고 메모리도 많이 사용하게 됩니다
• 이런 특별한 경우를 처리 할 수 있는 방법을 생각해내야 하는 문제는 처음 보는 문제였기에 이 방법을 익혀두기 위해 복습할 문제로 선정하였습니다.

** 코드는 더 보기 칸을 눌러서 확인해주세요 **

1. 압축되어있는 문자열을 압축되지 않은 상태로 되돌리기

• 괄호 안에 있는 숫자를 여는 괄호 바로 앞에 있던 숫자만큼 곱해줍니다. 괄호 안에 다시 괄호가 나올 경우 계속 괄호 앞쪽의 숫자를 체크하는 것이 번거롭기 때문에, 뒤쪽에서부터 탐색을 해줍니다.
• 뒤쪽에서부터 탐색을 하면 닫는 괄호가 나올때마다 스택에 담아주고 여는 괄호 다음의 숫자가 나오면 바로 바로 곱해주면서 풀어주면 되기 때문입니다.
• 여는괄호 다음에 나오는 숫자부터 닫는괄호 전까지의 숫자까지!!

S = input()

stack = []
N = len(S)
for i in range(N-1, -1, -1) :

    stack.append(S[i]) #뒤에서부터 일단 스택에 넣기
    if i == N-1 : continue
    # ) 가 나왔을 경우 앞으로 나올 값들은 (가 나온 이후의 숫자에 곱하기를 해줄 것
    if S[i+1] == "(" : # ( 다음에 숫자가 나왔을 경우 ) 가 나올때까지의 숫자들을 현재 값에 곱하기해줄것
        s = ""
        stack.pop() # 현재 숫자가 스택에 들어가 있을테니 빼주고
        stack.pop() # 그 다음은 여는 괄호이니 다시 빼준 뒤
        while stack :
            n = stack.pop() #그 다음 숫자부터 반복문을 돌리기
            if n == ")" : # 스택에 )가 나올때까지 돌려야함
                break
            else :
                s = s + n
        s *= int(S[i]) 
        stack.append(s) # 다음 괄호를 대비해서 스택에 문자열 다시 넣어두기

2. 문자열을 압축된 상태로 무턱대고 되돌릴 경우 길어지는 문자열, 시간초과 or 메모리 초과의 위험성 증가

• 우리가 필요한 건 문자열 전체가 아니라 문자열의 길이입니다.
• 100000000000000000000000000000 이라는 문자가 있다면 우리는 이 문자열이 필요한게 아니라 길이 30 필요하다는 걸 생각해야합니다
• 압축을 풀 때 굳이 압축이 풀린 문자열을 넣는게 아니라 문자열의 길이를 넣어주면 이 문제를 해결할 수 있습니다.
• 여는 괄호가 나왔을 때 처리해주는 부분을 살짝 바꿔보도록 하겠습니다.

if S[i+1] == "(" :
        s = 0 # s는 이제 문자열을 받는게 아니라 문자열의 길이를 받을 것
        stack.pop() 
        stack.pop()
        while stack :
            n = stack.pop()
            if n == ")" :
                break
            else :
                if type(n) == str : # 괄호 이후 문자열이 나올 때마다 길이 1 증가
                    s += 1
                else : # 문자열이 아니라면 구해놓은 길이가 나온것이므로 그만큼 증가
                    s += n
        stack.append(s * int(S[i])) # 길이를 모두 구했으면 다음 괄호를 대비해 다시 스택에 넣어두기

3. 괄호가 모두 끝났다면 기존에 남아있는 문자열이 계속해서 stack에 들어갔을 것이므로 stack에 있는 값들을 한 번 정리해줍니다. (기존에 주어지는 S의 길이는 50이기 때문에 stack에 들어있는 값들을 빼주는 건 큰 문제가 없습니다)

최종 코드

S = input()

stack = []
N = len(S)

for i in range(N - 1, -1, -1):
    stack.append(S[i])
    if i == N - 1:
        continue
    if S[i + 1] == "(":
        s = 0  # s는 이제 문자열을 받는게 아니라 문자열의 길이를 받을 것
        stack.pop()
        stack.pop()
        while stack:
            n = stack.pop()
            if n == ")":
                break
            else:
                if type(n) == str:  # 괄호 이후 문자열이 나올 때마다 길이 1 증가
                    s += 1
                else:  # 문자열이 아니라면 구해놓은 길이가 나온것이므로 그만큼 증가
                    s += n
        stack.append(s * int(S[i]))  # 길이를 모두 구했으면 다음 괄호를 대비해 다시 스택에 넣어두기

ans = 0
while stack:
    n = stack.pop()
    if type(n) == int:
        ans += n
    else:
        ans += 1

print(ans)

 - 문제 설명 - 

스-스-스도쿠 문제는  백트래킹을 활용하여 스도쿠를 풀어내는 문제입니다. 

백준 2580번 문제와 비슷하지만, 스도쿠가 만들어질 수 있는 경우만 만들어지는 2580번 스도쿠 문제와는 다르게 스-스-스도쿠는 스도쿠를 만들지 못하는 경우도 생깁니다.

스도쿠를 만드는 백트래킹 코드를 먼저 작성하고, 스도쿠를 만들지 못 할 경우를 조건으로 추가로 달아주면 되는 문제였습니다.

 복습할 문제 선정 이유 :

• 스도쿠를 만들지 못 할 경우를 체크했다고 생각하여 계속 틀린 답을 선택하게 되었습니다. 
• 처음에는 스도쿠를 푸는 로직을 백트래킹으로 수월하게 푸는 방법을 복습하려고 하였으나, 틀린 경우를 생각하는 습관도 기르고자 복습할 문제로 선정하였습니다.

** 코드는 더보기 칸을 눌러서 확인해주세요 **

1. 스도쿠를 풀어내는 로직 만들기

• 스도쿠의 빈 칸을 채워넣기 위해선 그 자리의 행과, 열과, 작은 사각형에 해당 칸의 값이 들어가지 않는 경우에 넣을 수 있습니다. 행, 열, 작은 사각형의 숫자들을 체크할 리스트를 만듭니다.

# 1. 9개 행의 숫자 입력받기
    sudoku = [list(map(int, input())) for _ in range(9)]
# 스도쿠에서 체크해야할 세가지
    r_check = [[False] * 10 for _ in range(9)]  # 가로 안에 들어갈 수 있는 숫자 체크하기 0~8번줄에 1~9까지의 숫자
    c_check = [[False] * 10 for _ in range(9)]  # 세로 안에 들어갈 수 있는 숫자 체크하기
    s_check = [[False] * 10 for _ in range(9)]  # 작은 사각형 안에 들어갈 수 있는 숫자 체크하기

• 스도쿠를 한 바퀴 돌면서 0이 아닌 숫자가 있는 경우 해당 칸의 행, 열, 작은 사각형에 숫자가 있다고 체크를 해줍니다. 이왕 한 번 반복하는김에 0인 경우도 나중에 백트래킹 처리를 위해 스택에 값을 넣어줍니다.

stack = []
# 스도쿠 돌면서 체크리스트 채워주기
    for i in range(9):
        for j in range(9):
            val = sudoku[i][j]
            if val != 0 :
                    r_check[i][val] = True  # i행 숫자 체크
                    c_check[j][val] = True  # j열 숫자도 체크
                    # 작은 사각형은 i//3*3 + j//3 번째 사각형이 된다
                    s_check[i // 3 * 3 + j // 3][val] = True
            else : # 0이 아닌 경우 백트래킹을 돌려야하므로 스택에 넣어준다
                stack.append((i, j))

• 스도쿠의 0인 칸들을 돌면서 백트래킹 실행 만약 True값 하나 찾았으면 다른 값들을 찾을 필요가 없는 backtracking을 만듭니다.
• 0이 존재하는 칸에 1~9를 넣어봅니다. 이 때 1~9까지 가능한 지 체크하기 위해서 이전에 만들어두었던 값들을 활용합니다.
• 스도쿠를 완성하지 못해 되돌아 왔을 경우, 넣어봤던 수들의 행, 열, 작은사각형 체크들은 다시 False로 바꿔주어야 한다는 것을 잊지 않습니다.

def backtracking(level):
    # 1. 종료조건
    if level == len(stack):
        return True
    else:
        for j in range(1, 10):  # 1~9까지의 숫자 넣어보기
            r, c = stack[level]  # r번째행 c번째 열에 있는 0 채워주기
            if not r_check[r][j] and not c_check[c][j] and not s_check[r//3*3 + c//3][j]:
                sudoku[r][c] = j  # 0 채워넣고
                r_check[r][j] = True  # 모든 행과 열과 작은사각형 방문처리 해준 뒤
                c_check[c][j] = True
                s_check[r // 3 * 3 + c // 3][j] = True
                if backtracking(level + 1):  # 다음 0 찾기(만약 찾아서 True 를 반환했으면 return True
                    return True
                else:  # 만약 다음 0을 못 찾고 돌아왔으면 다음 값을 넣어야하므로 모두 초기화
                    sudoku[r][c] = 0
                    r_check[r][j] = False
                    c_check[c][j] = False
                    s_check[r // 3 * 3 + c // 3][j] = False
    return False

2. 스도쿠가 가능하지 않은 경우 체크해주기

• 스도쿠가 불가능한 경우는 backtracking에서 True값을 반환하지 못하는 경우입니다. 

if backtracking(0) :
        for i in sudoku :
            print("".join(map(str, i)))
else :
    print("Could not complete this grid.")
print()

• 이렇게 처리해주고 다 풀었다~ 생각하면서 제출을 하면 틀렸습니다! 라는 문구를 볼 수 있어요.

• 스도쿠가 불가능 한 경우는 이렇게 넣을 수 있는 숫자가 없는 경우도 있지만, 문제 자체가 잘못 됐을 경우에도 스도쿠를 만들 수 없다는 것을 간과했습니다.
• 주어진 스도쿠 문제를 반복문으로 돌릴 때, 해당 열, 행, 작은 사각형에 숫자를 체크해주고, True로 바꿔주었습니다. 백트래킹을 할 때와 마찬가지로 처음에 보드에 스도쿠 문제로 주어진 숫자를 채워줄 때도, 숫자가 들어갈 수 있는지 체크를 해주어야합니다.
• 스도쿠 문제를 만들기 전에 조건을 걸어두어 불가능 한 경우 check 값을 추가해줍니다.

if not r_check[i][val] or not c_check[j][val] or not s_check[i // 3 * 3 + j // 3][val] :
                check = False
                break

최종 코드 

def backtracking(level):
    # 1. 종료조건
    if level == len(stack):
        return True
    else:
        for j in range(1, 10):  # 1~9까지의 숫자 넣어보기
            r, c = stack[level]  # r번째행 c번째 열에 있는 0 채워주기
            if not r_check[r][j] and not c_check[c][j] and not s_check[r//3*3 + c//3][j]:
                sudoku[r][c] = j  # 0 채워넣고
                r_check[r][j] = True  # 모든 행과 열과 작은사각형 방문처리 해준 뒤
                c_check[c][j] = True
                s_check[r // 3 * 3 + c // 3][j] = True
                if backtracking(level + 1):  # 다음 0 찾기(만약 찾아서 True 를 반환했으면 return True
                    return True
                else:  # 만약 다음 0을 못 찾고 돌아왔으면 다음 값을 넣어야하므로 모두 초기화
                    sudoku[r][c] = 0
                    r_check[r][j] = False
                    c_check[c][j] = False
                    s_check[r // 3 * 3 + c // 3][j] = False
    return False


T = int(input())

for tc in range(1, T + 1):
    # 1. 9개 행의 숫자 입력받기
    sudoku = [list(map(int, input())) for _ in range(9)]

    # 스도쿠에서 체크해야할 세가지
    r_check = [[False] * 10 for _ in range(9)]  # 가로 안에 들어갈 수 있는 숫자 체크하기 0~8번줄에 1~9까지의 숫자
    c_check = [[False] * 10 for _ in range(9)]  # 세로 안에 들어갈 수 있는 숫자 체크하기
    s_check = [[False] * 10 for _ in range(9)]  # 작은 사각형 안에 들어갈 수 있는 숫자 체크하기
    # 스도쿠에서 0인 곳 체크하기
    stack = []
    check = True
    # 스도쿠 돌면서 체크리스트 채워주기
    for i in range(9):
        for j in range(9):
            val = sudoku[i][j]
            if r_check[i][val] == True or c_check[j][val] == True or s_check[i // 3 * 3 + j // 3][val] == True :
                check = False
                break
            if val != 0 :
                r_check[i][val] = True  # i행 숫자 체크
                c_check[j][val] = True  # j열 숫자도 체크
                # 작은 사각형은 i//3*3 + j//3 번째 사각형이 된다
                s_check[i // 3 * 3 + j // 3][val] = True
            else:  # 0이면 스택에 넣어주기
                stack.append((i, j))
    if backtracking(0) and check :
        for i in sudoku :
            print("".join(map(str, i)))
    else :
        print("Could not complete this grid.")
    print()